Fuzzy search dictionary universal machine Levenshtein. Part 1

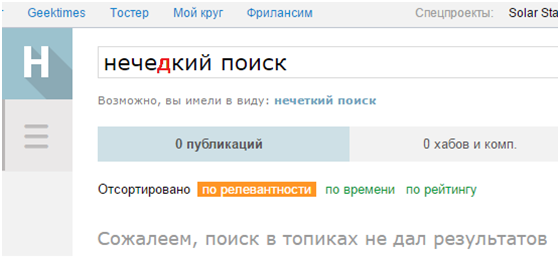
Fuzzy search of strings is very expensive in sense of computing resources by the task, especially if you require high accuracy of the results. The paper describes the fuzzy search algorithm in the dictionary, which provides high-speed search while maintaining 100% accuracy and relatively low memory consumption. Machine Levenshtein allowed the developers of Lucene to improve the speed of fuzzy searches two

the

Introduction

Fuzzy search of strings in the dictionary is the basis for building modern systems of spelling used in text editors, systems, optical character recognition and search engines. In addition, a fuzzy search is used in solving several computational problems of bioinformatics.

The formal definition of the problem of fuzzy search can be formulated as follows. For a given search query W you must select from the dictionary D a subset of P of all words, the measure of dissimilarity between R from the search query does not exceed some threshold value N:

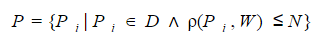
The degree of difference between two words can be measured, for example by distance Levenshtein or Arnulf-Levenshtein.

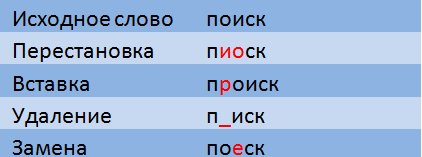
The Levenshtein distance is a measure of dissimilarity between two strings, defined as the minimum number of insertions, deletions and replacements of characters necessary for converting one string into the other.

When calculating the distance, Arnulf-Levenshtein to allow transposition (swapping two adjacent characters).

A few years ago on habré already there was a post from ntz devoted to fuzzy searching in the dictionary and the text — read more about the Levenshtein distances and the Arnulf-Levenshtein can be read there. I just remind you that the time complexity of checking the conditions
p(P_i, W)<=N using the dynamic programming methods is assessed as

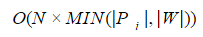
where |P_i|,|W| — the length of the string and query, respectively. Therefore, when solving practical problems a complete enumeration of the values in a dictionary, check each word, as a rule, inadmissible.

It should be noted that not every algorithm, a fuzzy search finds on request W all words D, satisfying p(P_i, W)<=N. So it makes sense to talk about the search precision as the number of found results to the actual number of words in the dictionary that meet a specified condition. For example, the precision search method n-gram author already mentioned by me post was estimated at 65%.

the

non-deterministic Levenshtein automaton

The author assumes that the reader is familiar with the basics of automata theory and formal languages, and will refrain from presenting the terms in this subject area. Instead I'll get straight to the point.

For the solution of practical problems uses deterministic finite automaton Levenshtein (to be completely accurate — his imitation). However, to understand the principles of operation of a deterministic finite automaton Levenshtein, it is better to consider the work of the non-deterministic version.

Automaton Levenshtein for the word W will be called finite state machine A_N(W) taking S then, and only then, when the Levenshtein distance (Arnulf-Levenshtein) between the words W and S does not exceed the specified value N.
A finite automaton Levenshtein for the words W and the allowed number of modifications N can be specified as an ordered five elements A_N(W)=<E,Q,Q₀,F,V> where:

E alphabet of the machine;
Q — the set of internal States;
q₀ — the initial state, belongs to the set Q;
F — the set of final or target States.
V — transition function, which determines what (what) state possible transition from the current state when receiving the input of the machine of the next character.

State of the nondeterministic automaton Levenshtein A_N(W) is denoted as i^#e where i=0..|W|, e=0..N. If the machine is in state i^#e, this suggests that the automaton is i “valid” characters and discovered e modifications. Because we are dealing with a machine that supports transposition (i.e., as p(S,W) is used, Arnulf distance-Levenshtein), the set of States must be supplemented by the States of {i_T^#e} where i=0..|W|-1, e=1..N.

The initial state is the state 0^#0.

Many final States includes state i^#e for which the condition |W| — i <= N — e.

Based on the physical meaning of the States in the automaton, it is easy to determine the composition of valid transitions. The function of the automaton Levenshtein is given in the table.

If you are interested in a strict mathematical substantiation of the States of the machine and above theses, you can find it in article Mihova and Schultz (2002).

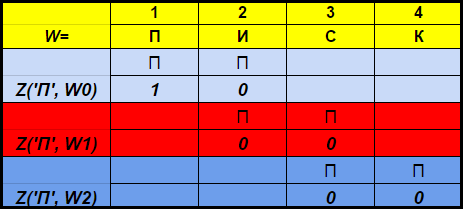
Characteristic vector Z(x, W_i) for x is called a bit vector of length min(N + 1, |W| — i), k-th element which is equal to 1 if (i+k)-th character of the string W is x and 0 otherwise. For example, W=”SQUEAK”
Z(‘P’, W₀ ) = <1, 0>, and Z(‘P’, W₁ ) = <0, 0>.

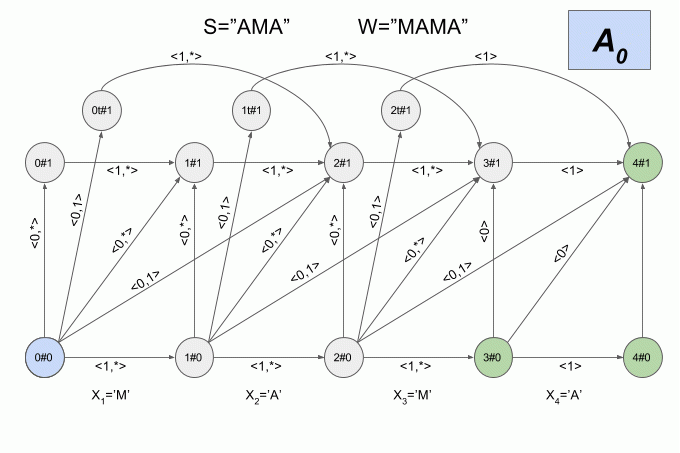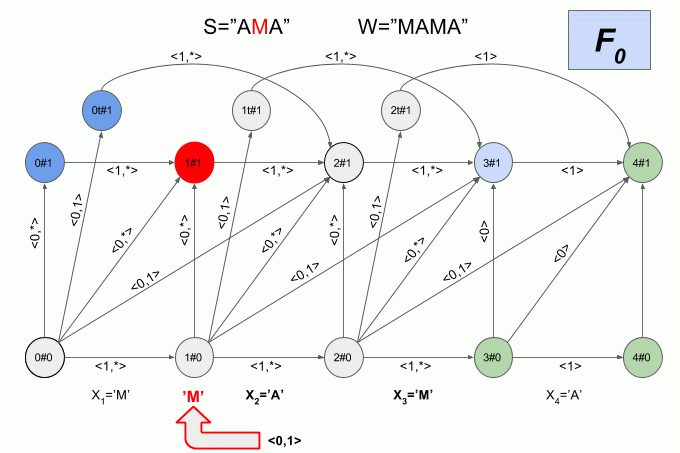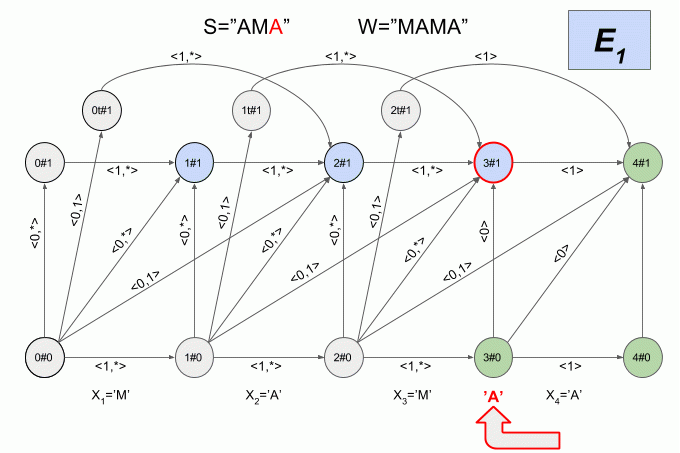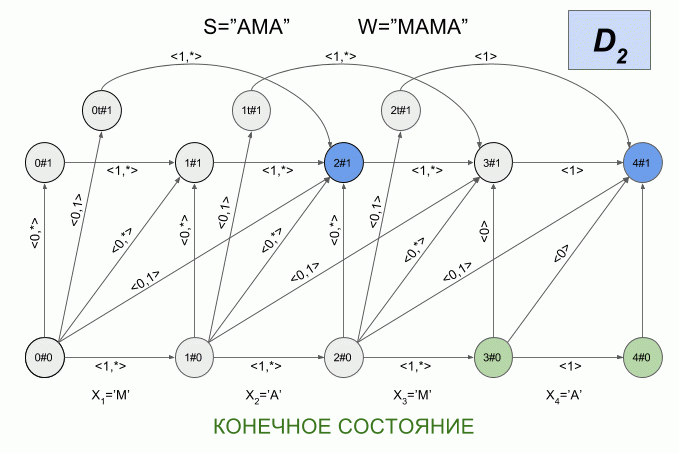
A graphical representation of the automaton Levenshtein W=”SQUEAK” and N=1 are shown in Fig. The transitions of the automaton signed the corresponding characteristic vectors.

The green highlighting shows the finite state machine. Light blue is the current (active) state machine.

The transition of the horizontal arrows is carried out when the machine entered the “correct” symbol.

The transition on the vertical arrows corresponds to the assumption that once introduced into the machine symbol is inserted in the original word W before (i+1)-m symbol. When you click on the vertical arrows automatic “detect” the modification of the word W — e while increasing 1.

The transition from the state i^#e as (i+1)^#e+1 corresponds to the assumption that the next symbol will substitute (i +1)-th character in the word W.

The transition from the state i^#e as (i + 2)^#e+1 corresponds to the assumption that the next character is (i + 2)-th character in the word W and (i + 1)-th character of the word W is omitted in the word S.

You've probably already guessed that the transition to the state i_T^#e suggests that the detected transposition (i + 1)and (i + 2)-th word characters W.

Now let's see how it works. The input to the machine is a new symbol I will denote the curved red arrow, and the right of the arrow indicate the value of the feature vector. So the machine A₁("SQUEAK") will work when you type in the words "SEARCH".

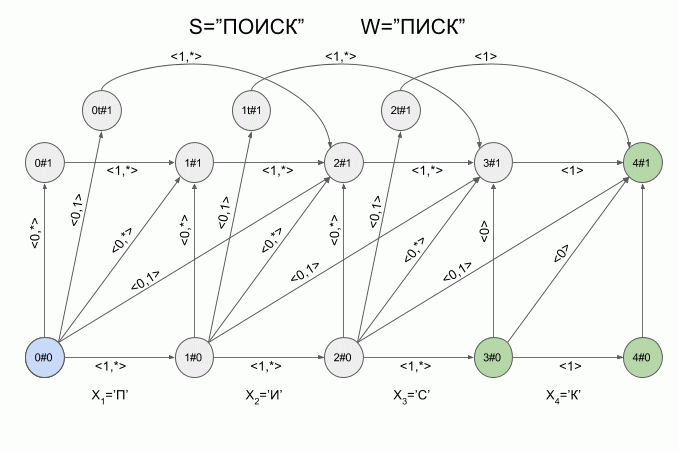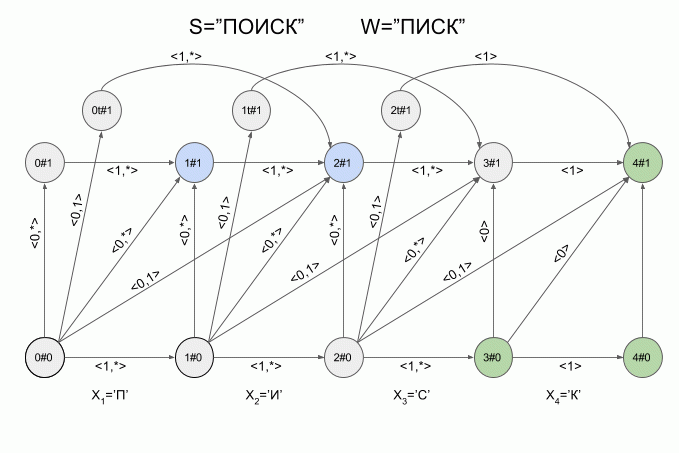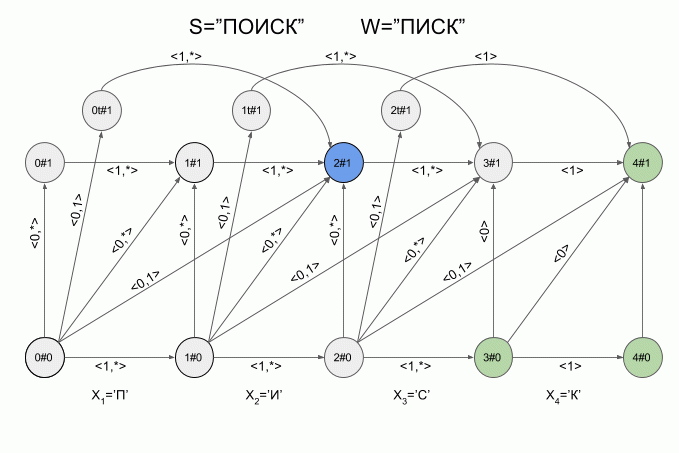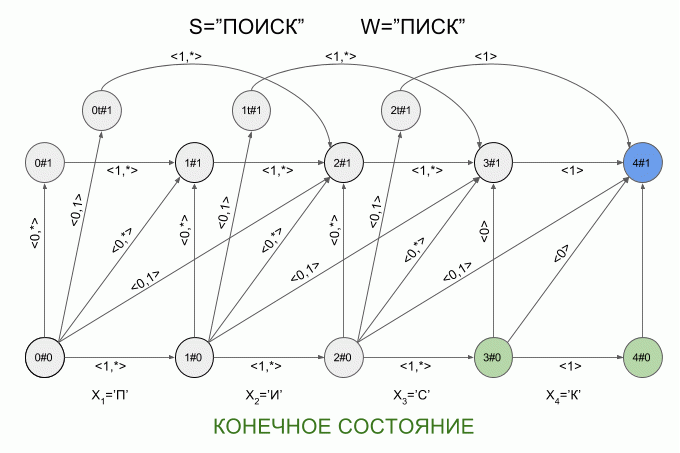
Please note, the actual sequence of state transitions of the automaton is not determined by the specific word applied to the input of the machine, but only a sequence of feature vectors. This sequence may be the same for two different words. For example, if the machine is set up on the word “mother”, then the sequence of characteristic vectors will be the same for the words “Lama”, “frame”, “lady”, etc.
Another interesting fact is that the structure of valid transitions of the machine does not change to i=0..|W| — (N+1).

These two circumstances make it possible with a software implementation of algorithms of fuzzy search to use not calculated for each particular word automatic, and universal imitation. That is why the title of the post refers to the “universal” machine Levenshtein.

Calculation of machine for specific words S is reduced in this case to a simple calculation of feature vectors for each character x word S. Change of state software is implemented as a simple increase of two variables e, i defined on the universal table size. Schulz and Mihov (2002) showed that the calculation of all characteristic vectors for the words S can be produced during O(|S|). This is the time complexity of the machine operation.

The symbolism of the word S is sequentially applied to the input of the machine. If after the filing of a certain symbol, it becomes clear that the distance between the lines S and W is greater than the threshold value N, the machine is in “empty” state is the active state of the machine are missing. In this case, you need to calculate the feature vectors for the remaining characters of the word S disappears.

So the machine “work” the word S=”X” under W=”SQUEAK”:

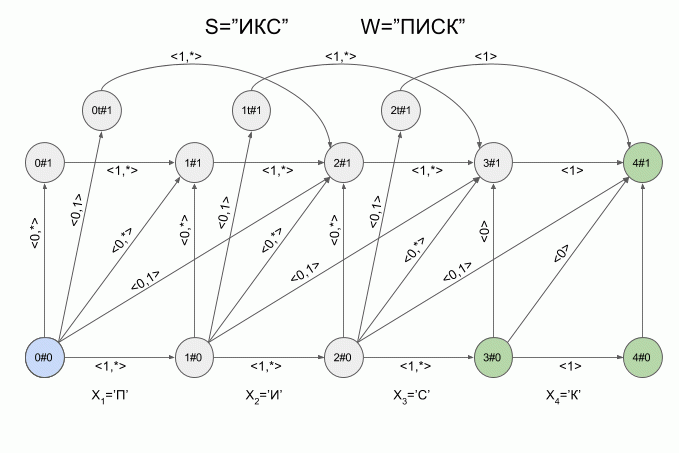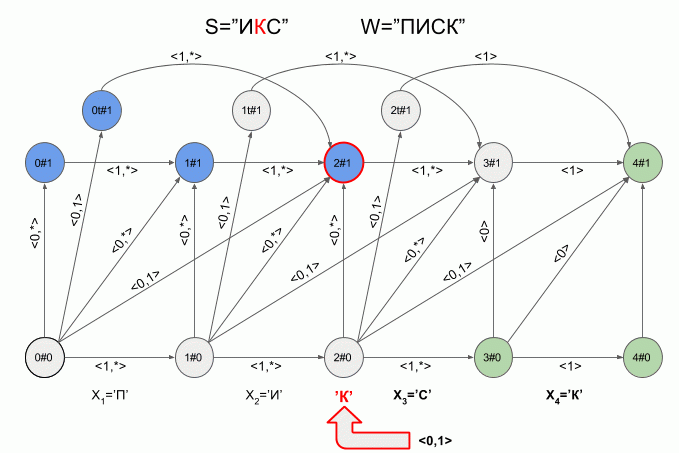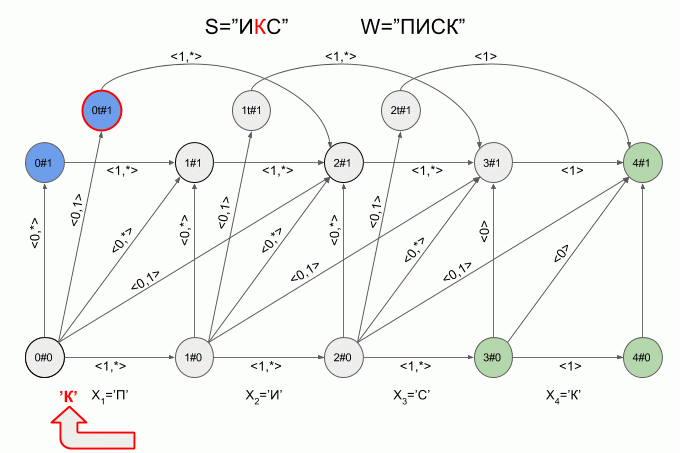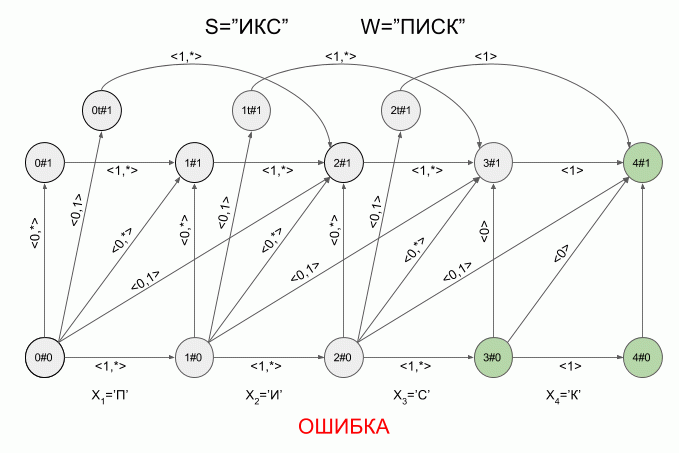
After a character is typed “And” in the machine appeared just four active state, but after entering the character “K” of the active States of the left machine was in error and did not accept the word “X”. The calculation of characteristic vectors for a symbol “s” not implemented.

the

Deterministic automaton Levenshtein

In accordance with a theorem on determinization for any automaton can be constructed equivalent deterministic finite automaton. Why do we need a deterministic automaton? Just at the software implementation it will work faster. Mainly due to the fact that can only have one current status and, as a consequence, when a letter is entered, it will be necessary to count only one feature vector and to define only one transition in the transition table.

If for the above nondeterministic automaton Levenshtein And₁(W) sequentially cycle through all possible values of the feature vectors, we can see that at the same time can be active state, the components of one of the following sets:

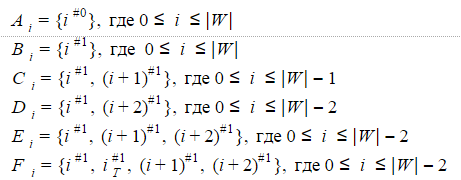
Six of the above sets and will represent the state of a deterministic Levenshtein automaton for N=1. More precisely, the machine will have six States for i=0..|W|-2, three States for i=|W|-1 and two States for i=|W|.

The dimension of the feature vector for a deterministic machine can be calculated as the 2N+1. Then the table of the automaton for a word of |W| letters with N=1 must have 2^2x1+1 strings and 6x(|W|-1)+3+2 the columns (for example, 8х35 for word 6 letters). In addition, such a table will have to count for each value in |W| separately. It is not very convenient and requires extra time to calculate or additional memory storage.

However, as I wrote above, the composition of valid transitions of the machine does not change to i=0..|W| — (2N + 1). Therefore, when software implementation is much easier to simulate a deterministic automaton instead of calculating the real. For this it is sufficient to store the value of the offset i and use the universal jump table with eight rows and six columns. Such a table can be calculated in advance.

With increasing i some state of the machine become unreachable, so i=|W|-2..|W| must be a single table of a smaller size.

Then, speaking of a deterministic Levenshtein automaton I will assume that is the above universal imitation.

With increasing N the number of States grows exponentially. So, for N=2 a deterministic automaton can have 42 state of N=3 is already a few hundred. And hence memory consumption will be proportional to O(N²).

The initial state of the deterministic Levenshtein automaton will be as A₀.

What kind of condition will end? Those that correspond to non-deterministic finite state machine. For N=1 it will be the state A_|W|, B_|W|, A_|W|-1, C_|W|-1, D_|W|-2, E_|W|-2, F_|W|-2.

Since the number of transitions between the six States is very large, and the physical meaning of the States of the deterministic automaton Levenshtein is not obvious, I will not give here a graphical representation. I think that the picture is not quite clear. If you still want to see it, you can find the article Mihova and Schultz (2004). I will give another example of a non-deterministic machine, but this time I will indicate in what state each moment is its deterministic equivalent.

the

a Software implementation of a deterministic automaton Levenshtein

A software implementation of the Levenshtein machine I wrote in C# that I am more familiar with this language. The source code you can find here. Universal transfer table is implemented as static fields of the class ParametricDescription. The class is represented in the universal table of transitions for N=1,2.

In addition to the tables, the class ParametricDescription also contains a table of increment displacement. Increment the offset is the value you want to increase the value i in the transition to the next state.

The machine itself Levenshtein implemented in the class LevTAutomataImitation. All class methods are very simple and I will not describe them in detail. When performing a fuzzy search in the dictionary, simply create one class instance per request.

Please note — the creation of a class instance LevTAutomataImitation is performed in a small constant time for any value W, S, N. In the instance of a class is stored, only the value of W and auxiliary variables of small size.

To select from the array of rows only those rows that are spaced from a predetermined distance, on the Arnulf-Levenshtein not more than 2, you can use the following code:

the

//Misspelled word
string wordToSearch = "fulzy";
//Your dictionary
string[] dictionaryAsArray = new string[] { "fuzzy", "fully", "funny", "fast"};
//Maximum Damerau-Levenstein distance
const int editDistance = 2;
//Constructing automaton
LevTAutomataImitation automaton = new LevTAutomataImitation (wordToSearch, editDistance);
//List of possible corrections
IEnumerable<string> corrections = dictionaryAsArray.Where(str => automaton.AcceptWord(str));

The given code implements a simple algorithm of fuzzy search using Levenshtein automaton — algorithm for complete enumeration. Of course, this is not the most efficient algorithm. A more efficient search algorithms using machine Levenshtein I'll explain in second part.

the

Поиск по этому блогу

computer express